
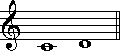
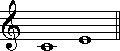
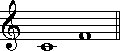
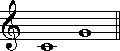
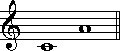
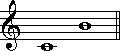
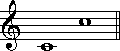
今回は、音程を取り上げます。音程とは、音と音の隔たりのこと。西洋音楽では、これを三度であるとか四度であるとかというように、度数でもって表します。数が少ないほど隔たりの幅は狭く、数が増えるほど幅は大きくなります。
ここで扱うのは、音程の表し方のみ、度数の数え方と音程の体系の説明だけに留めます。実際に鳴り響く音については、実践のなかでつかんでいくほうがよいでしょう。
音程というのは、音と音の隔たりのことを指します。同音を1度とし、ひとつ距離が離れるごとに度数が1度ずつ増していきます。例えば、ドと同音のドは1度であり、ドとレは2度となります。
このようにひとつずつ度数を増しいくと、8度で再び同じ音名に戻ります。当然ながら、これは同音ではありません。8度のことをオクターブと呼びます。
音程を測る基本となる単位、度数は、楽譜の線と間を単位とすると考えていただいてもかまいません。同じ線あるいは同じ間に示された二音は同音、つまり1度です。
ドを基準とした1度から8度までを、以下に例示しましょう。

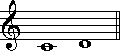
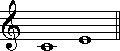
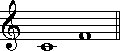
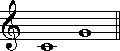
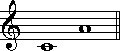
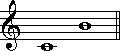
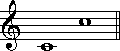
この例では、シャープやフラットといった臨時記号が付けられていませんが、仮に臨時記号が付いたとしても、度数は変わりません。
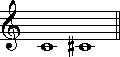

どちらも1度です。
臨時記号が付いても度数が変わらないことは説明しました。ですが、明らかに音程は異なるため、度数とは違う名称でもって、音程の違いを示します。
音程は、完全音程、長音程、短音程、増音程、減音程の五種に分けることができます。
完全音程に含まれる音程は、1度、4度、5度、8度です。これらは、それぞれ完全1度、完全4度、完全5度、完全8度と呼ばれます。
 (同音)
(同音)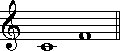 (5半音)
(5半音)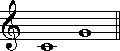 (7半音)
(7半音)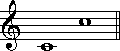 (オクターブ)
(オクターブ)例では、すべてドからの音程となっていますが、音程の幅さえ同じなら、どの音からはじめられても、同じく完全音程であるといえます。
長音程と短音程は、セットにして考えたほうがわかりやすいでしょう。長、短音程に含まれるのは、2度、3度、6度、7度です。
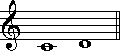 (2半音)
(2半音)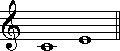 (4半音)
(4半音)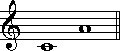 (9半音)
(9半音)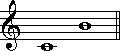 (11半音)
(11半音)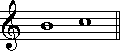 (1半音)
(1半音)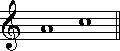 (3半音)
(3半音)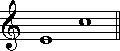 (8半音)
(8半音)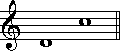 (10半音)
(10半音)長音程と短音程は、ちょうど半音分、隔たりの量が多いかどうかで決定されます。長音程の方が半音分隔たりが大きく、短音階は逆に小さくなります。
ミとファの間、シとドの間が、それぞれ半音だということを思いだして、もう一度よく例を見直してみてください。
増音程は、完全音程及び長音程にさらに半音分の隔たりの加えたものを指します。完全音程+半音、長音程+半音=増音程と考えていただくとわかりやすいです。
減音程は、増音程とは逆に、完全音程及び短音程から半音分の隔たりを減じたものになります。つまりは、完全音程−半音、短音程−半音=減音程といえます。
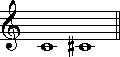
 (1半音)
(1半音)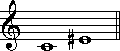 (5半音)
(5半音)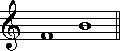 (6半音)
(6半音)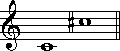 (13半音)
(13半音)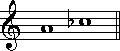 (2半音)
(2半音)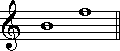 (6半音)
(6半音)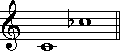 (11半音)
(11半音)増1度には注意してください。完全1度に対しシャープが付けられてもフラットが付けられても、どちらも半音分音程が広がっています。よって、両者とも増1度となるのです。
音程は、完全音程、長音程、短音程、増音程、減音程に分けられる。
完全音程に半音の増減があれば、増音程、減音程となる。同様に長音程に半音の増加で増音程、短音程に半音の減少で減音程ができる。
これら音程は、次のような関係にある。
減音程←完全音程→増音程
減音程←短音程←→長音程→増音程
なお、完全音程から長短音程は作りえない。逆も同様である。
本文で、具体的に音程の幅を示すために、音程それぞれが半音いくつ分であるかを付記していますが、この考え方は音楽的に大きく間違っています。なぜなら音程というのは、半音がいくつ、全音がいくつあるから何度、なのではなく、5度は5度、4度は4度。半音、全音は関係なく成立するものなのです。
音の高さは、振動数によって決定されます。音程は、この音の振動数の比率によって決まります。ここにある音があるとしましょう。この音の振動数を二倍にすると、その音はもとの音と1オクターブ(完全8度)の関係になります。つまり1オクターブとは、半音が12個あるのではなく、音の振動数比が、1:2である音程なのです。
じゃあ、他の音程はどういう振動数比を持つのでしょうか。
1:1、これは当然ながら同音、完全1度ですね。2:3の関係、これは完全5度になります。3:4は完全4度です。
4:5、これは長3度です。5:6は短3度。3:5が長6度になって、5:8は短6度になります。
そして8:9及び9:10の長2度、15:16の短2度。8:15の長7度、9:16の短7度。などなど、さらに続けることもできますが、このへんでやめておきましょう。
以上のように、音程というのはまず半音あるいは全音ありきではなくて、おおもとの音があって、もうひとつの音がその音とどういう関係にあるのかというものなのです(なお、二つの音の振動数比がそれぞれ単純な数であるほど、響きは純粋になり、協和しやすくなります)。本文での半音いくつという記述は、音程をわかりやすくするため、便宜上書かれたものであるので、皆さんは音楽をする際、こういう考え方をしては駄目ですよ。
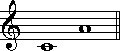 と
と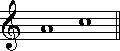 のように、両者が合わさることでオクターブができあがる音程を、補完音程といいます。この例は、6度(長6度)と3度(短3度)ですが、1度と8度、2度と7度、3度と6度、4度と5度がそれぞれ補完音程となっています。
のように、両者が合わさることでオクターブができあがる音程を、補完音程といいます。この例は、6度(長6度)と3度(短3度)ですが、1度と8度、2度と7度、3度と6度、4度と5度がそれぞれ補完音程となっています。
また、ド−ラとラードのように、どちらかの音がオクターブ位置をかえることででき音程を、転回音程といいます。
転回音程と補完音程は、同じものを指していると考えていただいて、ほぼ間違いありません。
完全音程は転回しても、完全音程のままです。完全4度が転回して生じた5度は、完全5度です。
長音程は、転回すると短音程に変わります。同様に、短音程を転回すると、長音程が生じます。前出の例において、長6度が転回し短3度になっていることに、注目してください。
長音程と短音程の関係と同様に、増音程は転回して減音程に、減音程は転回して増音程に変わります。
 (完全1度)←→
(完全1度)←→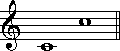 (完全8度)
(完全8度)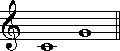 (完全5度)←→
(完全5度)←→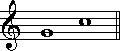 (完全4度)
(完全4度)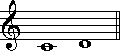 (長2度)←→
(長2度)←→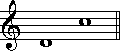 (短7度)
(短7度)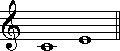 (長3度)←→
(長3度)←→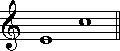 (短6度)
(短6度)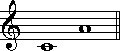 (長6度)←→
(長6度)←→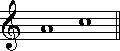 (短3度)
(短3度)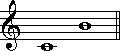 (長7度)←→
(長7度)←→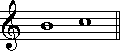 (短2度)
(短2度)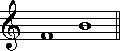 (増4度)←→
(増4度)←→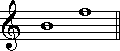 (減5度)
(減5度)音程がオクターブの範囲にとどまるものを単音程といい、オクターブを超えるものは複音程といいます。
単音程は、今まで提示してきた例で説明できます。すなわち、1度から8度(オクターブ)までが、単音程です。
複音程は、オクターブより大きな隔たりを持つもので、当然9度以上となります。
複音程の例をあげてみましょう。
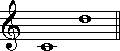
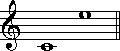
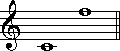
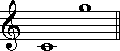 e.t.c.
e.t.c. 左から、9度、10度、11度、12度となります。
複音程は、九十十一と、数を増やしていく呼び方だけではなく、オクターブと何度という呼び方も同様に可能です。
先ほどの例ならば、左から、オクターブと2度、オクターブと3度、オクターブと4度、オクターブと5度となります。
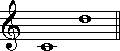
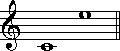
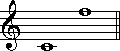
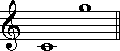
音程の開きは同じなのに、名前が違うという場合があります。次の例を見てください。
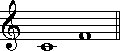
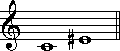
左は完全4度で、右は増三度です。名前の点においても、また楽譜上においても、ふたつは違う音程に見えます。ですが、このふたつは、五つの半音分の開きを持つ、同じ音程になります。
このような音程を、異名同音程といいます。
単音程における、異名同音程を網羅してみましょう。
それぞれがどういう音程であるかは、皆さんのほうで確かめてみてください。
異名同音程という、名前だけ違って実は同じ音程という現象。これ、厳密にいうと間違った理解です。というのは、異名同音程は異名同音というものの存在を前提としています。異名同音とは、例えばドのシャープとレのフラットやミとファのフラットが同じ音とされる約束のこと。でもこの考え方というのは、平均率という近代に成立した調律の方法に基づいたもので、この平均率を離れてしまうと、異名同音は存在しないため、異名同音程も存在しないということになってしまいます。
もう少し具体的に話しましょう。平均率は、一オクターブを均等に十二等分するという調律法で、結果としてすべての半音は同じ音程になります。ですが、この同音程とされている半音には、大半音という二つの音の幅が広いものと、小半音という狭いものの二種類が存在し、同様に全音にも大全音、小全音の区別があるのです。
例えば、ドとレの音程は長2度、レとミも長2度。でもこの二つの音程、厳密には違っています。ド-レは大全音で、レ-ミは小全音。この大全音と小全音がひとつずつ合わさって長三度になり、これは奇麗に調和します。C(ド)を主音とする二つの音階、ハ長調とハ短調。長調の第三音E(ミ)と短調の第三音Es(ミのフラット)の音程は小半音。長調のミとファは全半音で、違う音程となります。
大小全音、大小半音は微妙な差なのですが、人間にはきちんと聞き分けることができます。また、奇麗なハーモニーを作ろうと思えば、大小全半音の使い分けを避けて通ることはできません。心ある演奏家は、これは導音に当たる音だから高めに、とかいって、導音-主音(長調のシ-ド、短調のソ#-ラ)が小半音であることを意識的に演奏したりします。
このように、本来的には音の高さというのは、名前が違うと音高も違うというものなのです。すなわち、音程においても同様、異名になれば音程も異なります。異名同音や異名同音程というのは、近代の合理性に導かれた考え方なのです。
音程は、協和音程と不協和音程に分けることができます。
協和音程は、純正な響きを持つもの、ハーモニーを成立させるものと捉えられます。対して不協和音程は、響きを濁らせ、ハーモニーを乱すものであると捉えることができます。
この、協和と不協和の理論は、時代においても、また文化においても異なりますが、現在においては、以下に示す区分が一般的であるといえるでしょう。
時代によって協和、不協和という感覚は大きく異なってきました。一般的に不協和音程とされる7度ですが、現在の私たちからすれば、さほどに違和感なく受け容れられるはずです。私たちが日々聴いている音楽、ポップス、ロック、ジャズには、7度を加えられた和音が、自然に調和して響いているはず。9度、11度のテンションも珍しくなくなりました。それが私たちの時代の音楽です。
ではそれ以前はどうだったのでしょうか。ベートーヴェンやモーツァルトの時代においては、協和する和音として7度の加えられたものなど考えられなかったはずです。この時代の基本は三和音でした。ドミソやファラドといった、そういった和音が和声の根本にありました。3度や6度が、間違いなく協和音程として受け容れられていたのです。
ところが、その3度や6度は、中世ヨーロッパにおいては協和音程とは認められませんでした。この時代、協和する音程はさらに少なかったのです。九世紀頃、複数の声部を持つ楽曲が出現した当時には、完全1度、完全8度、完全5度そして完全4度だけが協和音程と認められるに過ぎませんでした。そしてこの考え方は、中世をほぼ通じて生きていました。
3度や6度音程が現れるのは、十四世紀頃にはいってからです。少しずつ姿を見せ始めたそれらは、ルネサンスを迎える頃には、広く使われるようになっていました。ルネサンス――十五世紀になってはじめて、三和音という響きは音楽の中にその位置を見つけたのでした。
楽譜あるいは音階上の半音の位置を把握することで、音程の判定は簡単なものとなります。例えば、二音間に半音がひとつ含まれる4度の場合、それは完全4度となります。含まれる半音がふたつなら、減4度になるわけです。
以下に、各度数ごとの判定の目安を、列挙します。なお音階上の半音の位置は、ミとファの間、シとドの間です。
臨時記号が付けられた場合は、適宜修正を加える必要があります。臨時記号による音程の変化は、前述の音程の名称のまとめを参照してください。
